A Fox's Guide to Geomorphs (Part 12)
There was something interesting that I noticed about the work of Keith J Davies yesterday.
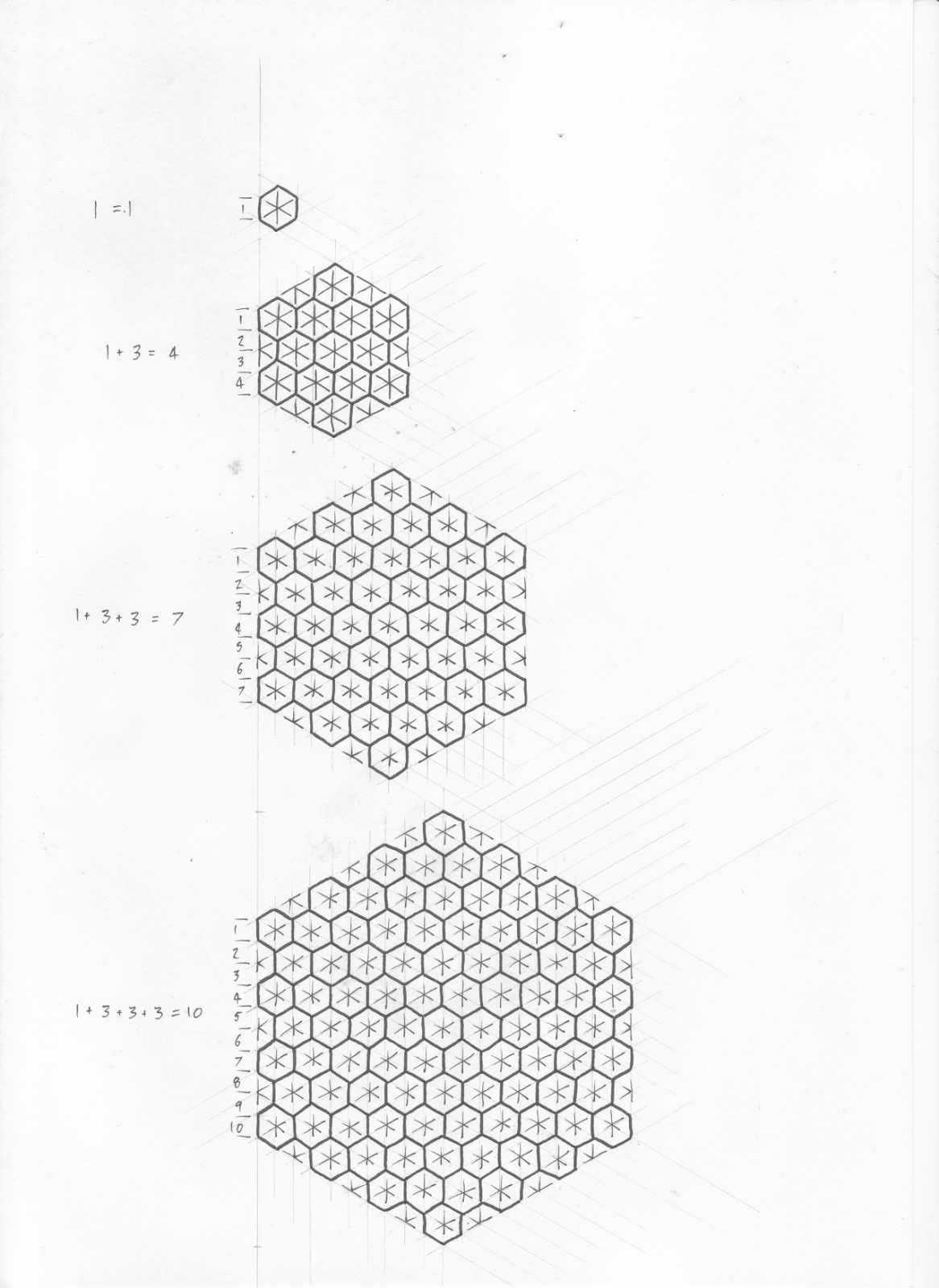
He divided the edges of the hex into tenths, then drew the isometric grid across it from these points. That's really interesting from the perspective of splitting a hexagonal geomorph into smaller geomorphs or building a larger hex from smaller hexes.
Basically, to do this effectively you need to divide the sides into a number of fragments equal to "one plus a multiple of three" (eg. 1 + 0x3 = 1, 1 + 1x3 = 4, 1 + 2x3 = 7, 1 + 3x3 = 10).
Here's an illustration to show what I mean.
It's not a specific element of geomorph design, it's just something to consider when it comes to scaling geomorphs (whether dividing larger geomorphs into smaller forms or combining smaller geomorphs into larger patterns). The fact that the 10 to 1 ratio makes things easier for those of us using metric is just a bonus.
He divided the edges of the hex into tenths, then drew the isometric grid across it from these points. That's really interesting from the perspective of splitting a hexagonal geomorph into smaller geomorphs or building a larger hex from smaller hexes.
Basically, to do this effectively you need to divide the sides into a number of fragments equal to "one plus a multiple of three" (eg. 1 + 0x3 = 1, 1 + 1x3 = 4, 1 + 2x3 = 7, 1 + 3x3 = 10).
Here's an illustration to show what I mean.
It's not a specific element of geomorph design, it's just something to consider when it comes to scaling geomorphs (whether dividing larger geomorphs into smaller forms or combining smaller geomorphs into larger patterns). The fact that the 10 to 1 ratio makes things easier for those of us using metric is just a bonus.
.png)

Comments